Today, we will begin with the first algorithm that everyone learns in their journey to become a Machine Learning Engineer. Before we jump into the topic, let's first discuss why linear regression?
It's simple and easy to understand
It's one of the most intuitive algorithms
It creates a base that will help you understand other algorithms easily
What is Linear Regression?
The most common definition that you might have heard of linear regression would be:
Linear Regression is a supervised machine learning algorithm that computes the relationship between one or more independent features and a dependent variable by fitting a linear equation to data.
Now, that's simple and fair enough. However, let's break it down to understand it.
A supervised learning algorithm, as in here we will have the input as well as the corresponding output(labels) available while training the model.
Independent features are the features that stand alone and are use to determine the value or calculate the value of any variable.
The dependent variable is the variable whose value we determine by using the independent features that we have.
Therefore, in this algorithm, we will simply find an equation that will give us the relationship between independent features and dependent variable.
Understanding Linear Regression
**Important:**Linear regression is used specifically for linear data.

Take a look at the given graph, you can see that the sales profit of ice-cream is linearly dependent on the temperature. It is obvious that the hotter the summer, the more you want to eat the ice-cream😋.
Now, using linear regression we can predict the sales of ice cream at a particular temperature. If you were to visually predict sales of ice cream at 60°F, you would have draw a line and checked the corresponding value on the y-axis as given below.

Therefore, now similarly, we must find a best-fit line that can perfectly represent the relationship between our data.
The equation of line is given by,
$$y = mx + b$$
where, y = the dependent variable(whose value we need to predict, i.e, sales of ice cream)
m = slope of the line
x = independent feature(that will help us find y, i.e, temperature)
b = intercept of the line
Significance of m
The m in the given equation of line represents the slope of the line, which means how much our value of y will change by unit change in x.
Now, if we keep b constant(b=0) and change the value of m, then the line will move about x axis as shown below.

The formula for slope of line is,
$$m = \frac{{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}}{{\sum_{i=1}^{n} (x_i - \bar{x})^2}}$$
Significance of b
In the given equation, b signifies the intercept of the line. It means that, it shows the value of y when m=0. Basically, it gives us the offset value.
When we keep m as constant(m=3) and change the value of b, we get the following results as shown by the animation. The line intersects y axis on different points based on value of b.

The formula for intercept is,
$$b = \bar{y} - m\bar{x}$$
Now, that you know equation of line and have the formula to calculate m and b, you can take random values for m and b and plot a line. Lets say, we assume a line to be best-fit line to our data. How would we know if the line is our best-fit line? That's excatly where cost function comes in the picture.
Cost Function
We can measure the errors produced by the line by calculating the distance between the actual value and the value predicted by line. From given figure, you can see that the dotted line shows that difference.

Therefore, our error function, which we call as our cost function, is the difference between the actual and predicted value. It is given by the below formula:
$$J(m, b) = \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - y_i)^2$$
We take square of the differences for mathematical simplicity and to emphasize on the large errors.
Now, since we know how much error our line is making, we must try to reduce that error.
Therefore, to minimize error you have two techniques:
Ordinary least square(Direct formula method)
Gradient Descent
We will be discussing gradient descent in the upcoming articles since its a vast and very interesting topic. We will now discuss only the Ordinary least square method here.
Before, we minimize error I will show you how the m and b decreases with the error function.
When we plot the value of error for different values of m, by keeping b constant, we get the following graph.

Similarly, by keeping m constant if we plot graph of E vs b, we get,

Finally, when we plot the changes in b vs m vs E, we get the following 3D graph,
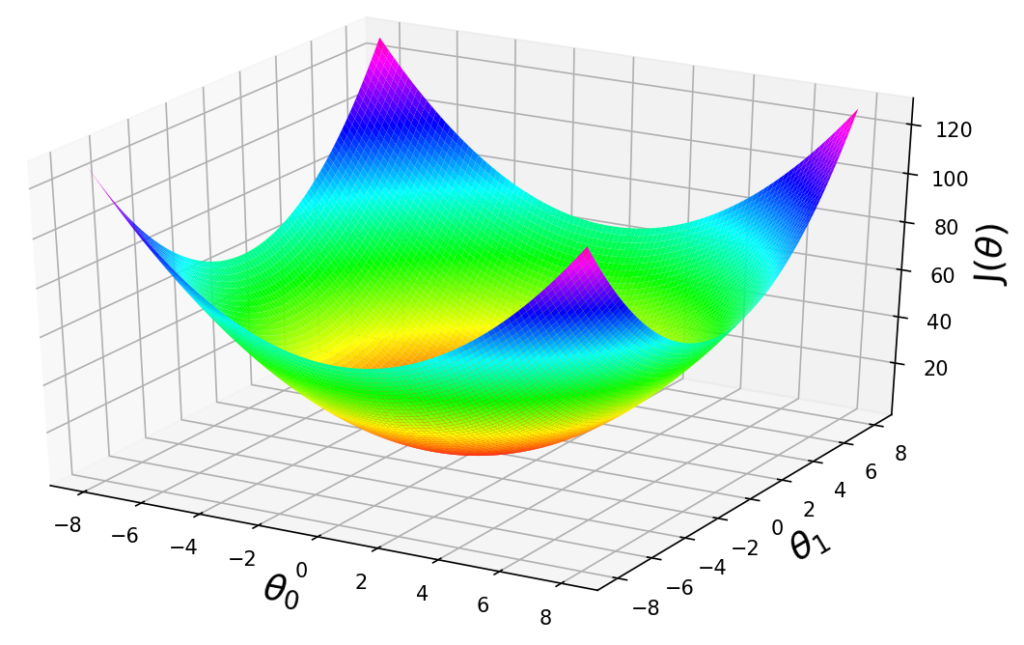
We know that value of any function is minimum when it's derivative is zero. Now, since we want the minimum value of the error function, we must differentiate it with respect to b and m and equate to zero.
Differentiating the error function with respect to b,
$$\begin{align*} \frac{\partial J(m, b)}{\partial b} &= \frac{\partial }{\partial b} \frac{1}{n} \sum_{i=1}^{n} (\hat{y}_i - mx_i - b)^2 = 0\\ &= \frac{-2}{n} \cdot \sum_{i=1}^{n}(\hat{y}_i - mx_i - b) = 0 \\ &= \sum_{i=1}^{n} \frac{\hat{y}_i}{n} - \frac{mx_i}{n} - \frac{b}{n} = 0 \end{align*}$$
Since,
$$\sum_{i=1}^{n} \frac{\hat{y}_i}{n} = \bar{y}, \sum_{i=1}^{n} \frac{mx_i}{n} = m\bar{x}, \sum_{i=1}^{n} \frac{b}{n} = n\frac{b}{n} = b$$
We have,
$$\bar{y} - m\bar{x}-b = 0 $$
$$b = \bar{y} - m\bar{x}$$
Differentiating the error function with respect to m,
$$\begin{align*} \frac{\partial J(m, b)}{\partial b} &= \frac{\partial }{\partial b} \sum_{i=1}^{n} (\hat{y}_i - mx_i - \bar{y} + m\bar{x})^2 = 0\\ &= -2 \cdot \sum_{i=1}^{n}(\hat{y}_i - mx_i - \bar{y} + m\bar{x}) (x_i - \bar{x}) = 0 \\ &= -2 \cdot \sum_{i=1}^{n}((\hat{y}_i - \bar{y}) - m(x_i + \bar{x})) (x_i - \bar{x}) = 0 \\ &= -2 \cdot \sum_{i=1}^{n}((\hat{y}_i - \bar{y})(x_i - \bar{x}) - m(x_i + \bar{x})^2) = 0 \\ &= \sum_{i=1}^{n}(\hat{y}_i - \bar{y})(x_i - \bar{x}) = m\sum_{i=1}^{n}(x_i + \bar{x})^2 \\ \end{align*} $$
$$m = \frac{\sum_{i=1}^{n}(\hat{y}_i - \bar{y})(xi - \bar{x}) }{\sum{i=1}^{n}(x_i + \bar{x})^2}$$
Thus, we have derived the formula for m and b. Now, the same thing is achieved in code as give below:
class MyLR:
def __init__(self):
self.m = None
self.b = None
def fit(self, X_train, y_train):
num = 0
den = 0
for i in range(X_train.shape[0]):
num += ((y_train[i] - y_train.mean())*(X_train[i] - X_train.mean()))
den += ((X_train[i] - X_train.mean())**2)
self.m = num/den
self.b = y_train.mean() - (self.m * X_train.mean())
print(self.m, self.b)
def predict(self, X_test):
print(self.m*X_test + self.b)
For studying the code of linear regression, you can refer to the kaggle notebooks given below:
https://www.kaggle.com/code/devyanichavan/my-linear-regression will help you understand how we can code linear regression from scratch
https://www.kaggle.com/code/devyanichavan/simple-linear-regression will guide you to use sklearn and create a simple linear regression model on your dataset
Conclusion
Thus, we have studied linear regression, infact you can say Simple linear regression as we worked with only one dependent and independent variable here. In the next article, we will be studying multiple linear regression in detail.
